Casa
four square theorem

Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers

Por um escritor misterioso

Descrição
Lagrange’s four-square theorem, in number theory, theorem that every positive integer can be expressed as the sum of the squares of four integers. For example, 23 = 12 + 22 + 32 + 32. The four-square theorem was first proposed by the Greek mathematician Diophantus of Alexandria in his treatise
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Lagrange's four-square theorem - Wikipedia
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Euclidean algorithm - Wikipedia
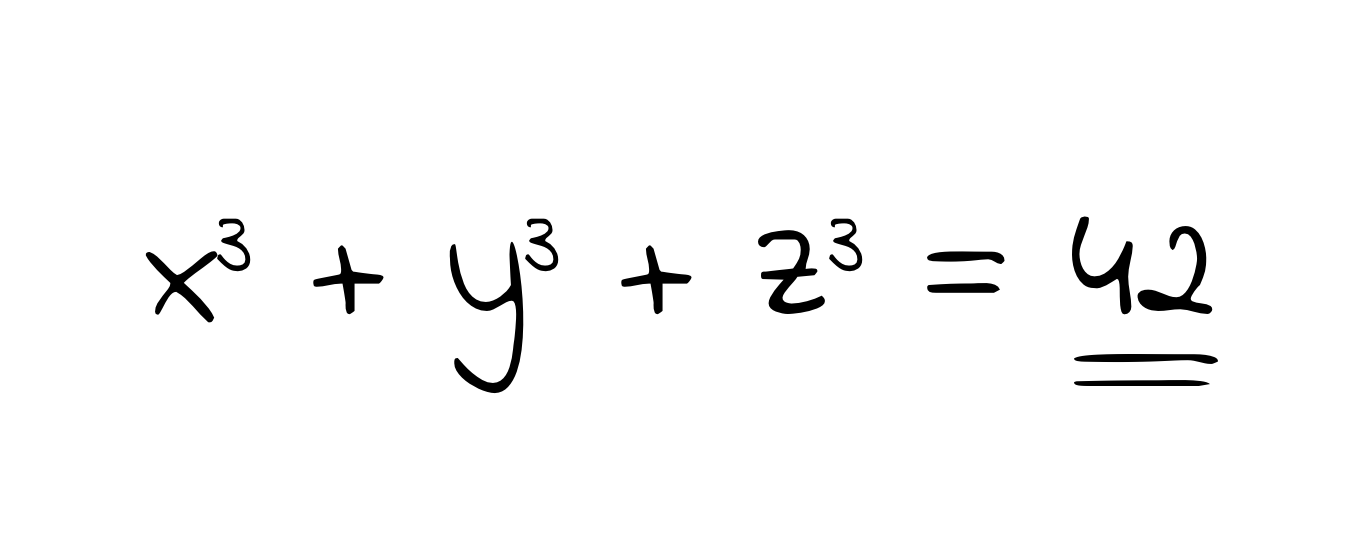
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Famous Diophantine Equations. A Diophantine equation is an algebraic…, by Jørgen Veisdal
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
PDF) New parametrization of $A^2+B^2+C^2=3D^2$ and Lagrange's four-square theorem
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
PDF) The Polynomial Solutions of Quadratic Diophantine Equation X 2 − p t Y 2 + 2 K t X + 2 p t L t Y = 0
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
PDF) New parametrization of A2 + B2 + C2 = 3D2 and langrange's four-square theorem
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Geometric Theorems, Diophantine Equations, and Arithmetic Functions by Don Hass - Issuu
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
PDF) The Quadratic Diophantine Equations x^2− P(t)y^2− 2P′(t)x + 4P(t)y + (P′(t))^2− 4P(t) − 1 = 0
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Quaternion algebra
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Introduction To Number Theory - Hill, PDF, Factorization
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
PDF) Small systems of Diophantine equations which have only very large integer solutions
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
PDF) On primitive solutions of the Diophantine equation x 2 + y 2 = M
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Table 3 from Extended Lagrange's four-square theorem
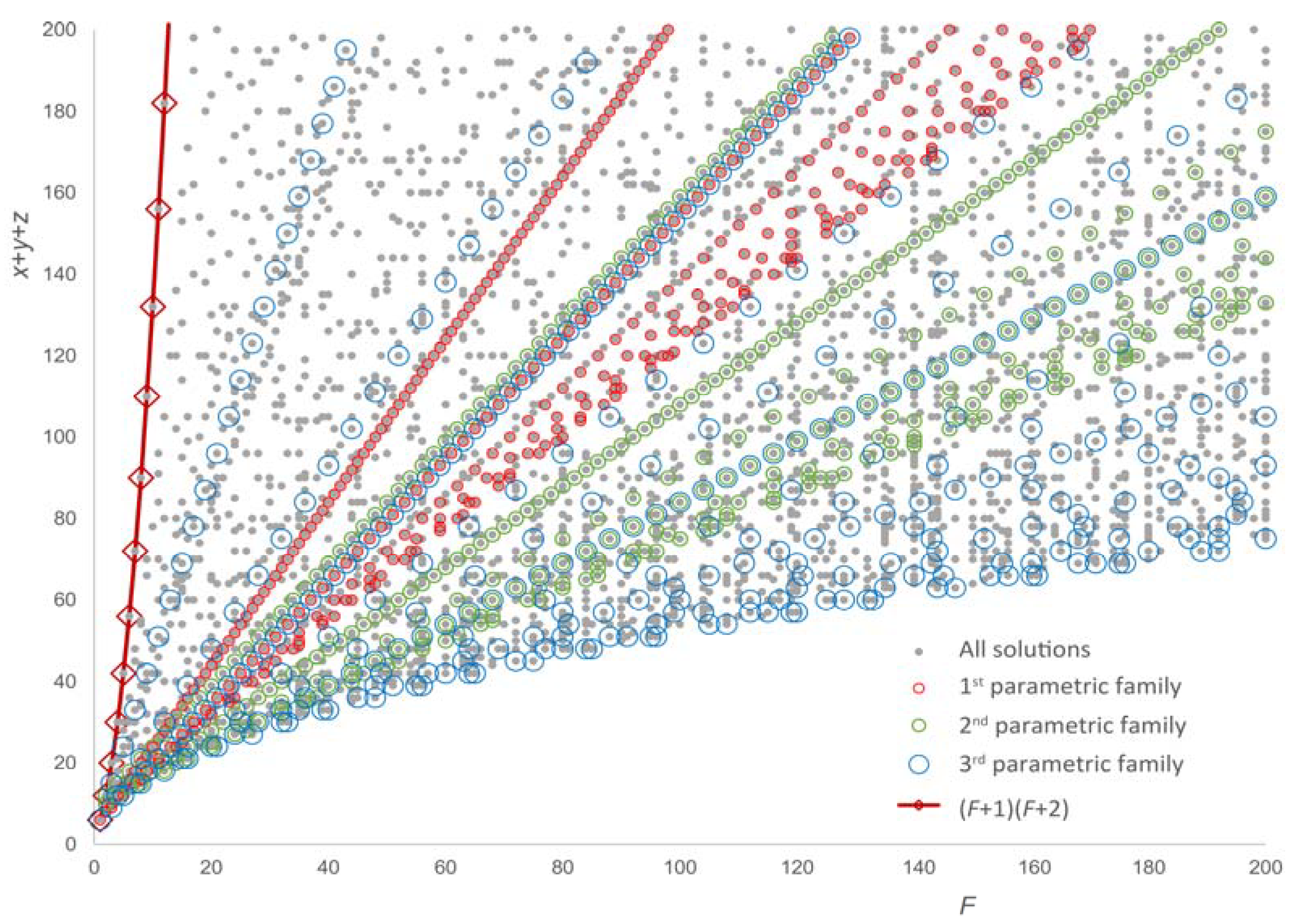
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers
Mathematics, Free Full-Text
de por adulto (o preço varia de acordo com o tamanho do grupo)